Review: Google's quantum error correction course
Late in 2024, the team at Google Quantum AI released a free online course on quantum error correction taught by Austin Fowler. I checked it out expecting “more of the same”, but it blew my mind and I literally couldn’t put it down until it was done. Here is a belated review, and a discussion of what made it work.
Hands-on quantum error correction with Google Quantum AI. Maciej’s score: 5/5.
My background in QEC
First, let me tell you a bit about my background, since how well a course lands depends very much on the target audience. I did my PhD in experimental physics, but over the last 4 years, I have spent most of my time at the intersection of experiments and theory. At my company we call this “system architecture”, and it essentially involves working across the stack to answer wacky questions such as “If our quantum computer is to be capable of providing quantum advantage on Ising model simulations, how hot can the ion trap chip get, and which technology can deliver appropriate cooling power.” As such, I understood QEC very well compared to a median experimentalist, and I could just about talk to a QEC expert without embarrassing myself - but I was never able to follow QEC conference talks very much.
In my PhD days at ETH Zurich, I have taught many master’s courses on quantum information, including a good chunk about QEC. I distinctly remember that in the 1st year of my PhD, my supervisor asked me to prepare a problem set specifically about fault-tolerance. I asked him if we had any materials, and he said “Not really… but I’m sure you’ll find something in Nielsen & Chuang”. In the end, I downloaded John Preskill’s notes and problem sets on fault tolerance, and decided to reuse them for the course. The only issue was that they came without solutions… So I did my best to solve as many of them as possible, sanity-checked with my supervisor that the solutions were not clear nonsense, and left many problems out as I didn’t really know how to tackle them ;) Hopefully, that gives you a sense of where I’m coming from.
The trouble with QEC courses
Watching from the sidelines, QEC always struck me as one of the most exciting and creative sub-fields of quantum computing. The issue is, however, that very few people have the background knowledge to even keep up with what’s going on. It’s not for the lack of trying - there are plenty of graduate-level QEC courses at various universities and summer/winter schools. In my experience, however, these courses finish well before they get to the fun stuff!
This is usually simply because there are sooooo many prerequisites to go through. Even if the lecturer only wants to talk about fault-tolerant magic state preparation techniques, you really want to first:
- Remind people how gates and state vectors work, such that you can…
- Talk about density matrices, such that you can…
- Explain CTP maps and Kraus operations, such that you can…
- Talk about noise digitization, such that you can…
- Talk about parity checks, such that you can…
- Talk about the X-correcting Shor code, such that you can…
- Talk about the X and Z correcting Shor code, such that you can…
- Talk about stabiliser codes, such that you can…
- Talk about the Earnst-Knill theorem, such that you can…
- Talk about error propagation, such that you can…
- Talk about fault tolerance, such that you can…
- Talk about T-gate teleportation, such that you can
- Talk about magic states.
It’s unlikely you can get through this list in a single course - and you haven’t even learned anything about the surface code!
Enter Google
Google’s QEC course flips this upside down. 20 minutes in, you are told that operations are matrices, errors are matrices, and errors are of X and Z type. 10 minutes later, you’ve built your first repetition code:

Notice already a major deviation from how this course approached the repetition code vs how most of this is taught. Traditionally, students start by only considering errors on computational qubits, and assume ancillas and measurements are perfect. The idea of measurement errors is only brought up when talking about fault tolerance. Here, no distinction is made between gate and measurement errors. A qubit is a qubit, an operation is an operation, that’s it. This allows them to introduce the notion of repeated measurements and detectors early on. I found this to be a huge conceptual simplification compared to the standard treatment.
5 minutes later, we are decoding our first errors through minimum-weight perfect matching:

In most courses, the concept of a decoder is not even mentioned - there is a box that computes what needs to happen in response to syndromes, end of story. But so much of modern QEC research is about finding data- and compute-efficient decoding schemes. The Google team makes it clear that there is no QEC without a decoder - and they are correct!
10 minutes of video later, we’ve learned all about stabilisers. This is a pretty standard treatment, but excitingly, it moves very quickly from algebraic to pictorial representation. The vibe is really that the pictorial representation is the right one, and it provides a natural segway to the surface code:
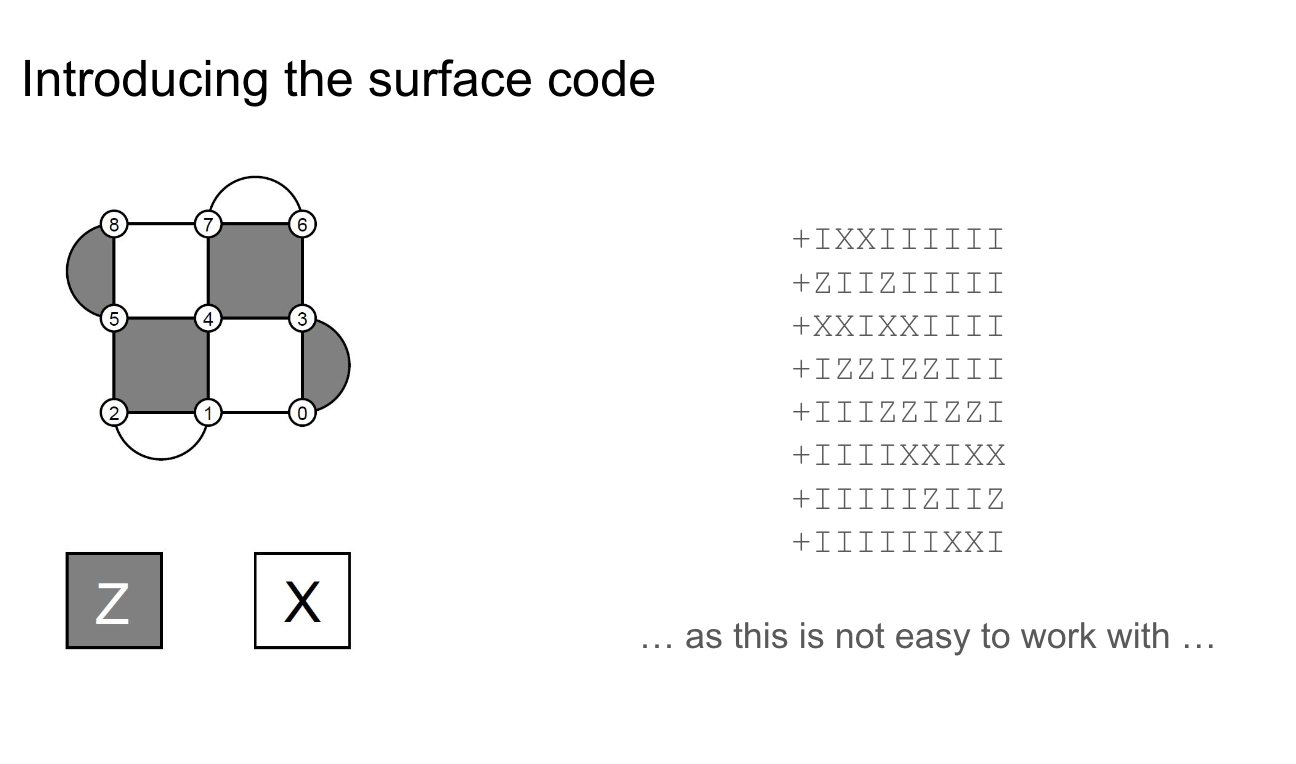
The lecture then quickly goes through examples of error propagation in the surface code, 10 minutes later building up to a pretty complete description of the surface code memory experiment. Wow!

The course ends with a thorough tutorial on simulating logical circuits with STIM, and an advanced introduction to Crumble, an automated error-propagation tool written by Craig Gidney.
This makes me think…
Taking a step back… Between watching videos, reflecting, and completing assignments, the course took me perhaps 8 hours from start to finish (ok, I skipped some of the Crumble part). That’s probably equivalent workload to 1-2 lecture + problem set sessions we did at ETH. Yet after the Google course, I feel sort of capable of reading modern QEC papers and watching modern talks. That’s pretty remarkable!
Of course, this is not to say that the Google course is “better”. Rather, it is simply extremely practical and hands-on. It makes the assumption that most students are willing to accept statements like “quantum operations can be represented as matrices” and are most interested in cool ideas that make QEC work - and that the curious ones can easily look up “what these matrices mean”.
It reminds me very much of the broad distinction between the “American-style” vs “Soviet-style” education. Around 2010, I left my home country of Poland to study at the University of Oxford. Every few months, I’d come back and compare notes on the physics we were learning with my friends who stayed back home. The most striking distinction was the UK’s focus on practicality, vs Poland’s focus on foundations. Pretty much on day 1 in Oxford, someone hands you a booklet that says “This is how you differentiate, this is how you integrate, now let’s go solve some differential equations”. This is in stark contrast to Poland, where you spend one semester learning about limits, and the second semester defining a derivative… by the time you start solving real-world equations, you’re an old man!
(Funny aside: when I went to Oxford for the first time for an interview, I was given a limit to calculate. I said what any well-educated Polish kid would say: “Let me start by checking if the limit really exists”. I got a lot of confused laughs!)
All in all, while this course is not for everyone, I believe it is a shockingly efficient way of getting from “zero to hero” in QEC. And I hope to see more content like this out there! If quantum technologies are to truly take off as an engineering discipline, we need practical, to-the-point teaching resources that can bring you up to speed with modern techniques. I hope Google’s QEC course sets an example that many will follow.
If you also completed Google’s QEC course, I would love to know what you thought! Also, if you know any other courses of this kind, drop me a line - I would love to check them out.